The total mechanical energy of an airplane in flight is the sum of its potential energy from altitude and kinetic energy from airspeed. The potential energy is expressed as mgh, and the kinetic energy as ½ mV². Thus, the airplane's total mechanical energy can be stated as:
mgh + ½ mV²
Where,
m = mass
g = gravitational constant
h = height (altitude)
V = velocity (airspeed)
A flying airplane is an “open” energy system, which means that the airplane can gain energy from some source (e.g., the fuel tanks) and lose energy to the environment (e.g., the surrounding air). It also means that energy can be added to or removed from the airplane’s total mechanical energy stored as altitude and airspeed.
The indicated altitude displayed in the altimeter and its associated potential energy are based on the height of the airplane above a fixed reference point (mean sea level or MSL), not on the height above ground level (AGL), which changes with variations in terrain elevation. Likewise, the indicated airspeed displayed in the airspeed indicator and its associated kinetic energy are based on the speed of the airplane relative to the air, not on the speed relative to the ground below, which varies with changes in wind speed and direction.
Note that changes in indicated altitude and airspeed are attained through forces resulting from the pilot’s direct manipulation of the controls. These direct control inputs determine the airplane’s ability to climb/descend or accelerate/decelerate. In contrast, changes in AGL-altitude and groundspeed are affected by “external” factors, such as varying terrain elevation and wind, which the pilot cannot alter. Of course, the pilot should manipulate the airplane’s energy in such way as to minimize any risks associated with terrain or wind. For example, the pilot may seek to manipulate energy state so as to maximize the airplane’s energy gains and minimize energy loses when faced with rising terrain. A safer heading may also be an option.
Once airborne, the airplane gains energy from the force of engine thrust (T) and it loses energy from aerodynamic drag (D). The difference between energy in and out (T – D) is the net change, which determines whether total mechanical energy—stored as altitude and airspeed—increases, decreases, or remains the same.
When thrust exceeds drag (T – D > 0), the airplane's total mechanical energy increases. The pilot can store the surplus energy as increased altitude or airspeed. For example, if the pilot decides to put all the surplus energy into altitude, the airplane can climb at a constant airspeed. [Figure 1A] If the pilot opts to place all the surplus energy into airspeed, the airplane can accelerate while maintaining altitude. [Figure 1B]
Energy can also be exchanged between altitude and airspeed. For example, when a pilot trades airspeed for altitude, as altitude increases, airspeed decreases. In other words, when energy is exchanged, altitude and airspeed always change in opposite directions (absent any other energy or control inputs). As one goes up, the other one comes down. Also note that even though the distribution of energy over altitude and airspeed may change dramatically during energy exchange, the total amount of mechanical energy can remain the same at the end of the exchange maneuver [Figure 1F], as long as thrust is adjusted to match drag as the latter varies with changes in airspeed.
PS = (T – D)V/W
Where,
T = Thrust
D = Drag
V = velocity (airspeed)
W = aircraft weight
More importantly, there is a fundamental relationship between changes in the airplane’s total energy resulting from this net energy flow on one hand, and changes in the energy stored as altitude and airspeed on the other. This fundamental relationship can be summarized through the airplane’s energy balance equation. [Figure 2]
The left side of the energy balance equation represents the airplane’s net energy flow, while the right side reflects matching changes to the energy storage. Thus, changes to the airplane’s total energy affect the left side of the equation, while the right side shows possible changes in energy distribution between altitude and airspeed.
Note that a change in total energy resulting from the difference between thrust and drag (left side) always matches the change in total energy redistributed over altitude and airspeed (right side). Although rate of energy change, expressed as specific excess power (PS), varies during flight—becoming positive, negative, or zero—both sides of the equation are inexorably balanced regardless of whether the airplane is accelerating, decelerating, climbing, descending, or maintaining constant altitude and airspeed. (Note: This simplified balance equation does not account for long-term changes in total mechanical energy caused by the reduction in aircraft weight as fuel is gradually burned in flight. Although the effect of weight loss on total energy becomes critical when solving long-term aircraft performance problems such as range and endurance, it is negligible when considering short-term flight control problems.)
Of course, the pilot controls the change in total energy on the left side of the equation, as well as the distribution of any changes in energy over altitude and airspeed on the right side. How the pilot coordinates the throttle and elevator to achieve and maintain desired altitude and airspeed targets as well as avoid energy "crises" is at the core of energy management.
RELATED POSTS
mgh + ½ mV²
Where,
m = mass
g = gravitational constant
h = height (altitude)
V = velocity (airspeed)
A flying airplane is an “open” energy system, which means that the airplane can gain energy from some source (e.g., the fuel tanks) and lose energy to the environment (e.g., the surrounding air). It also means that energy can be added to or removed from the airplane’s total mechanical energy stored as altitude and airspeed.
A Frame of Reference for Managing Energy State
At any given time, the energy state of the airplane is determined by the total amount and distribution of energy stored as altitude and airspeed. Note that the pilot’s frame of reference for managing the airplane’s energy state is airplane-centric—being a function of indicated altitude and indicated airspeed, and not height above the ground or groundspeed.The indicated altitude displayed in the altimeter and its associated potential energy are based on the height of the airplane above a fixed reference point (mean sea level or MSL), not on the height above ground level (AGL), which changes with variations in terrain elevation. Likewise, the indicated airspeed displayed in the airspeed indicator and its associated kinetic energy are based on the speed of the airplane relative to the air, not on the speed relative to the ground below, which varies with changes in wind speed and direction.
Note that changes in indicated altitude and airspeed are attained through forces resulting from the pilot’s direct manipulation of the controls. These direct control inputs determine the airplane’s ability to climb/descend or accelerate/decelerate. In contrast, changes in AGL-altitude and groundspeed are affected by “external” factors, such as varying terrain elevation and wind, which the pilot cannot alter. Of course, the pilot should manipulate the airplane’s energy in such way as to minimize any risks associated with terrain or wind. For example, the pilot may seek to manipulate energy state so as to maximize the airplane’s energy gains and minimize energy loses when faced with rising terrain. A safer heading may also be an option.
Once airborne, the airplane gains energy from the force of engine thrust (T) and it loses energy from aerodynamic drag (D). The difference between energy in and out (T – D) is the net change, which determines whether total mechanical energy—stored as altitude and airspeed—increases, decreases, or remains the same.
When thrust exceeds drag (T – D > 0), the airplane's total mechanical energy increases. The pilot can store the surplus energy as increased altitude or airspeed. For example, if the pilot decides to put all the surplus energy into altitude, the airplane can climb at a constant airspeed. [Figure 1A] If the pilot opts to place all the surplus energy into airspeed, the airplane can accelerate while maintaining altitude. [Figure 1B]
 |
| Figure 1 A-F. Examples of typical energy transactions |
When drag exceeds thrust, (T – D < 0), the airplane's total mechanical energy decreases. The pilot has two sources of stored energy to tap into. For example, the pilot may choose to let the airplane descend at a constant airspeed [Figure 1C)] or slow down while maintaining altitude [Figure 1D] as stored energy is withdrawn to deal with the energy deficit. When energy gained equals that lost (T – D = 0), all thrust is spent on drag. In this case, the total amount of mechanical energy and its distribution over altitude and airspeed does not change. Both remain constant as the airplane maintains a constant altitude and airspeed. [Figure 1E]
Energy can also be exchanged between altitude and airspeed. For example, when a pilot trades airspeed for altitude, as altitude increases, airspeed decreases. In other words, when energy is exchanged, altitude and airspeed always change in opposite directions (absent any other energy or control inputs). As one goes up, the other one comes down. Also note that even though the distribution of energy over altitude and airspeed may change dramatically during energy exchange, the total amount of mechanical energy can remain the same at the end of the exchange maneuver [Figure 1F], as long as thrust is adjusted to match drag as the latter varies with changes in airspeed.
Managing Energy is a Balancing Act
Since the airplane gains energy from engine thrust (T) and loses energy through aerodynamic drag (D), energy flows continuously into and out of the airplane while in flight. Usually measured as Specific Excess Power (PS), or rate of energy change, the net energy flow is a direct function of the difference between thrust and drag.PS = (T – D)V/W
Where,
T = Thrust
D = Drag
V = velocity (airspeed)
W = aircraft weight
More importantly, there is a fundamental relationship between changes in the airplane’s total energy resulting from this net energy flow on one hand, and changes in the energy stored as altitude and airspeed on the other. This fundamental relationship can be summarized through the airplane’s energy balance equation. [Figure 2]
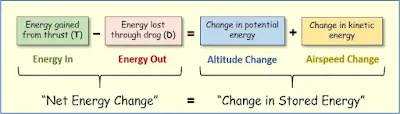 |
| Figure 2. The energy balance equation |
The left side of the energy balance equation represents the airplane’s net energy flow, while the right side reflects matching changes to the energy storage. Thus, changes to the airplane’s total energy affect the left side of the equation, while the right side shows possible changes in energy distribution between altitude and airspeed.
Note that a change in total energy resulting from the difference between thrust and drag (left side) always matches the change in total energy redistributed over altitude and airspeed (right side). Although rate of energy change, expressed as specific excess power (PS), varies during flight—becoming positive, negative, or zero—both sides of the equation are inexorably balanced regardless of whether the airplane is accelerating, decelerating, climbing, descending, or maintaining constant altitude and airspeed. (Note: This simplified balance equation does not account for long-term changes in total mechanical energy caused by the reduction in aircraft weight as fuel is gradually burned in flight. Although the effect of weight loss on total energy becomes critical when solving long-term aircraft performance problems such as range and endurance, it is negligible when considering short-term flight control problems.)
Of course, the pilot controls the change in total energy on the left side of the equation, as well as the distribution of any changes in energy over altitude and airspeed on the right side. How the pilot coordinates the throttle and elevator to achieve and maintain desired altitude and airspeed targets as well as avoid energy "crises" is at the core of energy management.
RELATED POSTS
